

Mathematics-Online course: Preparatory Course Mathematics - Linear Algebra and Geometry - Systems of Linear Equations

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Preparatory Course Mathematics - Linear Algebra and Geometry - Systems of Linear Equations | ||
Gauss Elimination to Echelon Form | ||
| [previous page] [next page] | [table of contents][page overview] |
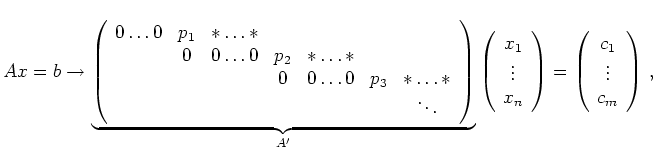
In detail the ![]() -th elimination step
proceeds as follows:
-th elimination step
proceeds as follows:
If there is no possible pivot, the echelon form is reached.
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 1/9/2017 |