

Mathematics-Online course: Preparatory Course Mathematics - Linear Algebra and Geometry - Systems of Linear Equations

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Preparatory Course Mathematics - Linear Algebra and Geometry - Systems of Linear Equations | ||
Matrix | ||
| [previous page] [next page] | [table of contents][page overview] |
A
![]() -matrix over field
-matrix over field ![]() is a set of numbers from
is a set of numbers from ![]() arranged in a rectangular grid as follows:
arranged in a rectangular grid as follows:
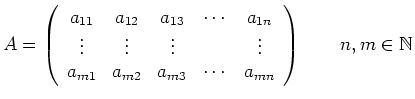
![]() is called
is called ![]() -th row vector of
-th row vector of ![]() .
.
![]() is called
is called ![]() -th column vector of
-th column vector of ![]() .
.
| Observe: | 1st index = row index |
| 2nd index = column index |
A
![]() -matrix is called column vector.
-matrix is called column vector.
Row vectors as well as column vectors can be considered as elements
of ![]() and vice versa.
The set of all
and vice versa.
The set of all
![]() -matrices is denoted by
-matrices is denoted by
![]() .
.
According to the above remark we have
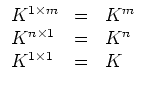
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 1/9/2017 |