

Mathematics-Online course: Basic Mathematics - Complex Numbers

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Basic Mathematics - Complex Numbers | ||
Division of Complex Numbers | ||
| [previous page] [next page] | [table of contents][page overview] |
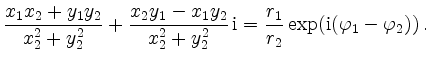
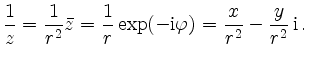
A complex number's reciprocal can be
constructed via reflection at the unit circle
![]() , as is illustrated in the following figure.
, as is illustrated in the following figure.
![\includegraphics[height=6cm]{a_division_bild}](/inhalt/aussage/aussage380/img6.png)
The complex conjugate
![]() is the intersection of
the diagonals of the quadrilateral formed by
the tangents at
is the intersection of
the diagonals of the quadrilateral formed by
the tangents at ![]() passing through
passing through ![]() and the
perpendicular radii.
The number
and the
perpendicular radii.
The number ![]() is then obtained by reflection at the
real axis.
is then obtained by reflection at the
real axis.
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 10/31/2008 |