

Mathematics-Online course: Basic Mathematics - Complex Numbers

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Basic Mathematics - Complex Numbers | ||
Gaussian Plane | ||
| [previous page] [next page] | [table of contents][page overview] |
![\includegraphics[width=0.4\moimagesize]{a_gausssche_bild1}](/inhalt/aussage/aussage378/img2.png)
![\includegraphics[width=0.4\moimagesize]{a_gausssche_bild2}](/inhalt/aussage/aussage378/img3.png)
In polar coordinates, the Euler-Moivre-formula yields the representation
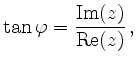
In the table below some complex numbers are given in polar coordinates.
|
|
|
|
|
|||
| 0 |
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 10/31/2008 |