

Mathematics-Online course: Basic Mathematics - Combinatorics

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Basic Mathematics - Combinatorics | ||
Factorial | ||
| [previous page] [next page] | [table of contents][page overview] |
The number ![]() corresponds to the number of possibilities to
arrange n distinct objects.
corresponds to the number of possibilities to
arrange n distinct objects.
For large ![]() , the asymptotic behavior of
, the asymptotic behavior of
![]() can be approximated by Stirling's formula:
can be approximated by Stirling's formula:
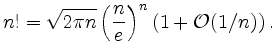
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 10/31/2008 |