

Mathematics-Online course: Basic Mathematics - Natural Numbers

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Basic Mathematics - Natural Numbers | ||
Mathematical Induction | ||
| [previous page] [next page] | [table of contents][page overview] |
Statements with natural numbers as their parameters can be proved by
the Principle of Mathematical Induction.
If ![]() is a statement
that depends on
is a statement
that depends on
![]() ,
the method of proof consists of the following
two steps:
,
the method of proof consists of the following
two steps:
The Principle of Mathematical Induction successively infers the
truth of a statement ![]() from the previous statement
from the previous statement ![]() .
Therefore, if in the base step
.
Therefore, if in the base step ![]() is verfied
for some
is verfied
for some ![]() rather than
rather than ![]() ,
then the statement has only been proved for
,
then the statement has only been proved for
![]() .
.
The formula for the sum of square numbers,
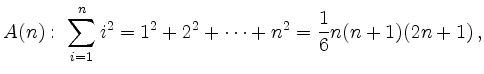
Base step (![]() ):
):
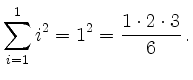
Conclusion (
![]() :
:
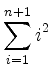 |
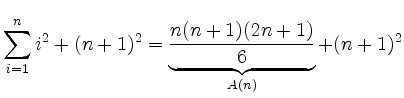 |
||
![$\displaystyle \displaystyle\frac{(n+1)\big[n(2n+1)+6(n+1)\big]}{6}
= \displaystyle\frac{(n+1)(n+2)(2n+3)}{6}\,.$](/inhalt/beispiel/beispiel52/img8.png) |
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 10/31/2008 |