

Mathematics-Online lexicon: Annotation to

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: Annotation to | ||
Riemann Integral | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
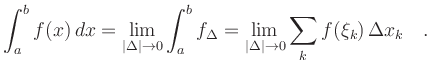
![\includegraphics[width=0.6\linewidth]{riemann_bild}](/inhalt/aussage/aussage154/img8.png)
For a positive function ![]() ,
,
![]() corresponds to the area
below the graph of
corresponds to the area
below the graph of ![]() .
.
For a sequence
![]() of partitions with
of partitions with
![]() ,
we compare the Riemann sums corresponding to
,
we compare the Riemann sums corresponding to ![]() and
and ![]() with the aid of a partition
with the aid of a partition ![]() , which consists of the union of the
points of
, which consists of the union of the
points of ![]() and
and ![]() :
:
![$\displaystyle \sum_{j=1}^k f(\zeta_j)\,\Delta z_j,\quad
\zeta_i\in[z_{i-1},z_i]
\,,
$](/inhalt/erlaeuterung/erlaeuterung66/img8.png)
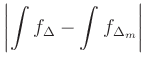 |
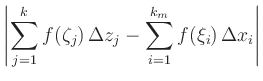 |
||
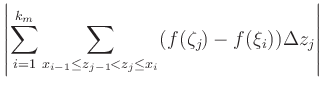 |
|||
![$\displaystyle \vert\Delta_m\vert\,
\underbrace{\max_{t\in[a,b]} \vert f^\prime(...
...um_{i=1}^{k_m}
\sum_{x_{i-1}\le z_{j-1}<z_{j}\le x_{i}}
\Delta z_j
}_{=b-a}
\,,$](/inhalt/erlaeuterung/erlaeuterung66/img15.png) |
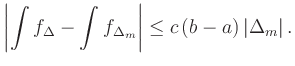
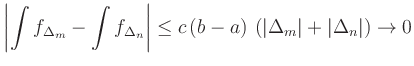 for
forThe convergence of two sequences to the same limit can be established with an identical argument.
For piecewise continuous ![]() , the proof is technically more complicated.
It relies on the uniform continuity of
, the proof is technically more complicated.
It relies on the uniform continuity of ![]() on the closed interval of
integration:
on the closed interval of
integration:
| automatisch erstellt am 22. 9. 2016 |