

Mathematics-Online lexicon: Annotation to

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: Annotation to | ||
Tensor Products of Integration Rules | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
Integration rules for rectangles
![\includegraphics[width=0.5\linewidth]{Bild_Rechteck_Quadratur}](/inhalt/aussage/aussage1484/img2.png)
If the formulas
![]() for approximating
for approximating
![]() are exact for polynomials of degree
are exact for polynomials of degree ![]() ,
then the product rule
,
then the product rule
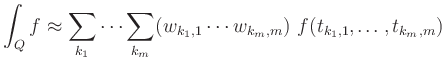
For simplicity, we consider functions of two variables
(![]() ).
To this end we denote by
).
To this end we denote by
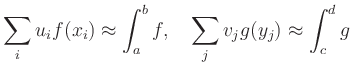
![$\displaystyle s = \sum_i u_i \left[ \sum_j v_j
f(x_i,y_j) \right]
\,.
$](/inhalt/erlaeuterung/erlaeuterung646/img3.png)
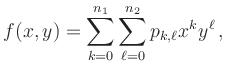
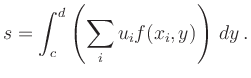
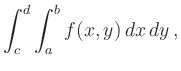
| automatisch erstellt am 17. 1. 2017 |