A farmer employs 25 workers and wishes to optimize the
cattle breading on his 120 hectare of meadland.
He assumes that 10 sheep require 1 hectare and 10
cows 3 hectare of land.
Moreover, he calculates 1 worker per 40 sheep and per
20 cows, respectively.
His profit is 100 EUR per sheep and 250 EUR per cow.
How should the farmer partition his meadowland,
if he takes into account that the state pays a
premium of 500 EUR per hectare for land set-aside?
The mathematical formulation of this problem is
Eliminating 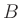 with the aid of the second equation
and rewriting the inequalities as well as
the target function yields
with the aid of the second equation
and rewriting the inequalities as well as
the target function yields
i.e., a linear program
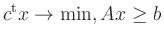 with
with
In the figure, the admissible set is bounded by
and the target function
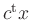 increases in the
direction of the gradient
increases in the
direction of the gradient 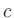 .
Since
.
Since 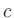 is perpendicular to the line through
is perpendicular to the line through
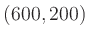 and
and 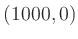 , the entire segment
from
, the entire segment
from 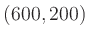 to
to 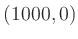 is optimal.
Hence, the farmer maximizes his profit, if all workers
are needed and if he keeps at least 600 sheep.
is optimal.
Hence, the farmer maximizes his profit, if all workers
are needed and if he keeps at least 600 sheep.
| |
automatisch erstellt
am 26. 1. 2017 |


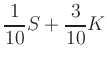
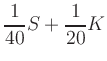
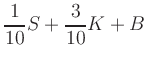
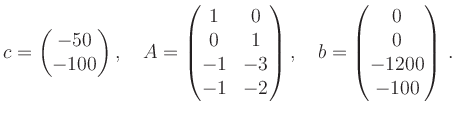
![\includegraphics[width=0.5\linewidth]{bsp_lineares_programm1}](/inhalt/beispiel/beispiel604/img23.png)