Mathematik-Online lexicon: Canteen

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematik-Online lexicon:
	Canteen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

overview

The menu of the canteen shows fish and stew. The cook should maximize the total profit, taking the following into account.

Deducting the material costs, the revenues are 50 cent per fish and 1 dollar per stew.
At most 1000 dishes can be prepared.
For 300 portions of fish the eat-by date threatens to expire; they have to be used immediately.
Since some remains have to be salvaged, at least 200 portions of stew should be cooked.

To transform the problem to standard form, we replace the constraint ,,number of dishes $\leq 1000$ `` by ,,-(number of dishes $\geq -1000$ `` With , denoting the portions of fish and stew, respectively, we obtain the problem

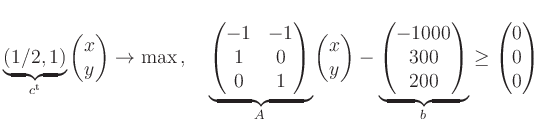
$\displaystyle \underbrace{(1/2,1)}_{c^{\operatorname{t}}}\begin{pmatrix}x \\ y\... ...00 \\ 300\\ 200\end{pmatrix}}_{b} \geq \begin{pmatrix}0 \\ 0\\ 0\end{pmatrix}$

According to the characterization of maxima, there exist Lagrange mulipliers $\lambda$ , $\sigma$ , $\rho$ $\le 0$ with

$\displaystyle \frac{1}{2}$	$\displaystyle =$	$\displaystyle - \lambda + \sigma$
$\displaystyle 1$	$\displaystyle =$	$\displaystyle - \lambda+\rho$
$\displaystyle \lambda (x_\star+y_\star - 1000)$	$\displaystyle =$	0
$\displaystyle \sigma (x_\star - 300)$	$\displaystyle =$	0
$\displaystyle \rho (y_\star - 200)$	$\displaystyle =$	0

Choosing $\lambda = 0$ leads to the contradiction $\rho = 1$ . Hence, $x_\star + y_\star = 1000$ . Choosing $\sigma = 0$ implies $\lambda = -\frac{1}{2}$ , $\rho = \frac{1}{2}$ , and thus leads to a contradiction as well. Therefore, $x_\star = 300$ , and we obtain the solution

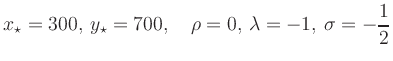
$\displaystyle x_\star = 300,\, y_\star = 700,\quad \rho = 0,\, \lambda =- 1,\, \sigma = -\frac{1}{2}$

This means, the cook should prepare 300 portions of fish and 700 portions of stew.

The solution of this simple example can also be constructed geometrically.

$\includegraphics[width=0.5\linewidth]{Bild_Beispiel_Mensa}$

To determine the optimal corner $(x_\star,y_\star)$ , we move a level line of the target function (dashed) in the direction of the gradient until it ceases to intersect the admissible region.

[Links]

automatisch erstellt am 26. 1. 2017