
Mathematics-Online lexicon:
|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Real Fourier-Series | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
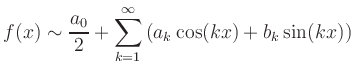
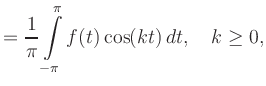 |
||
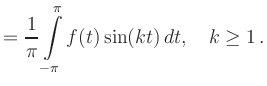 |
A convergent Fourier series needs not to represent the true function value at every point.
Usually, at a point of discontinuity, the series converges to the arithmetic mean of the left and right limits of ![]() .
This explains the notation
.
This explains the notation
![]() instead of
instead of
![]() ,
which emphasizes these convergence issues.
,
which emphasizes these convergence issues.
see also:
| automatically generated 9/22/2016 |