

Mathematics-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Integrating Factor | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
If a differential equation of the form
becomes exact by multiplication with a function ![]() then
then ![]() is called an integrating factor of the differential equation.
is called an integrating factor of the differential equation.
Note that it follows that
In general integrating factors are not easy to find. Sometimes it is possible
to find an integrating factor ![]() which depends only on
which depends only on ![]() (or only on
(or only on
![]() ).
).
The condition on an integrating factor depending only on ![]() is
is
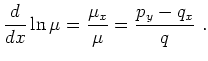
This can be solved, if the right hand side
![]() is only a
function of
is only a
function of ![]() In this case it follows that
In this case it follows that
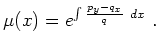
Similarly integrating factors depending only on ![]() may be determined if they
exist.
may be determined if they
exist.
Example:
| automatically generated 7/ 5/2005 |