

Mathematics-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Surface Integral | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
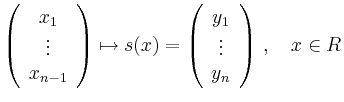
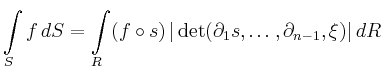
Weaker conditions on the smoothness of ![]() and
and ![]() are possible by defining the
integral as a suitable limit. Also the surface can be composed of several smaller
ones. In this case the integral over the region is the sum over the integrals of the
smaller surfaces.
are possible by defining the
integral as a suitable limit. Also the surface can be composed of several smaller
ones. In this case the integral over the region is the sum over the integrals of the
smaller surfaces.
Examples:
| automatically generated 5/30/2011 |