

Mathematics-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Linear Program | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
For the concrete example
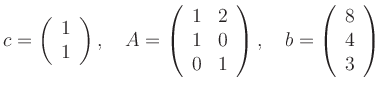
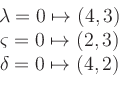
![\includegraphics[width=0.4\linewidth]{Bild_Lineares_Programm}](/inhalt/aussage/aussage690/img26.png)
The figure illustrates a geometric construction of the
solution.
The solution ![]() is the point where a level
line of the target function touches the shaded
admissible region.
Clearly, the target function increases (decreases) if
the level lines begin to intersect (not intersect)
the admissible region.
is the point where a level
line of the target function touches the shaded
admissible region.
Clearly, the target function increases (decreases) if
the level lines begin to intersect (not intersect)
the admissible region.
see also:
| automatically generated 1/26/2017 |