

Mathematics-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Euclidean Normal Forms of Three-Dimensional Quadrics | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
conical quadrics
| normal form | name |
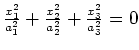 |
point |
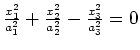 |
(double) cone |
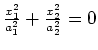 |
line |
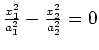 |
intersecting planes |
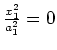 |
coincident planes |
central quadrics
| normal form | name |
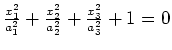 |
(empty set) |
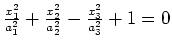 |
hyperboloid of 2 sheets |
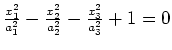 |
hyperboloid of 1 sheet |
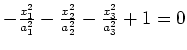 |
ellipsoid |
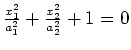 |
(empty set) |
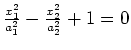 |
hyperbolic cylinder |
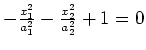 |
elliptic cylinder |
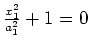 |
(empty set) |
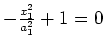 |
parallel planes |
parabolic quadrics
| normal form | name |
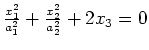 |
elliptic paraboloid |
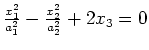 |
hyperbolic paraboloid |
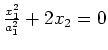 |
parabolic cylinder |
The normal forms are uniquely determined up to permutation of subscripts
and in the case of conical quadrics up to multiplication by a constant
![]() .
.
The values ![]() are set to be positive and are called lengths of
the principal axes of the quadric.
are set to be positive and are called lengths of
the principal axes of the quadric.
| (double) cone | intersecting planes |
![\includegraphics[width=.4\moimagesize]{quadriken_kegel}](/inhalt/aussage/aussage665/img20.png) |
![\includegraphics[width=.4\moimagesize]{quadriken_schneidende_ebenen}](/inhalt/aussage/aussage665/img21.png) |
| hyperboloid of 2 sheets | hyperboloid of 1 sheet |
![\includegraphics[width=.4\moimagesize]{quadriken_zweischaliges_hyperboloid}](/inhalt/aussage/aussage665/img22.png) |
![\includegraphics[width=.4\moimagesize]{quadriken_einschaliges_hyperboloid}](/inhalt/aussage/aussage665/img23.png) |
| ellipsoid | hyperbolic cylinder |
![\includegraphics[width=.4\moimagesize]{quadriken_ellipsoid}](/inhalt/aussage/aussage665/img24.png) |
![\includegraphics[width=.4\moimagesize]{quadriken_hyperbolischer_zylinder}](/inhalt/aussage/aussage665/img25.png) |
| elliptic cylinder | elliptic paraboloid |
![\includegraphics[width=.4\moimagesize]{quadriken_elliptischer_zylinder}](/inhalt/aussage/aussage665/img26.png) |
![\includegraphics[width=.4\moimagesize]{quadriken_paraboloid}](/inhalt/aussage/aussage665/img27.png) |
| hyperbolic paraboloid | parabolic cylinder |
![\includegraphics[width=.4\moimagesize]{quadriken_hyperbolisches_paraboloid}](/inhalt/aussage/aussage665/img28.png) |
![\includegraphics[width=.4\moimagesize]{quadriken_parabolischer_zylinder}](/inhalt/aussage/aussage665/img29.png) |
see also:
| automatically generated 7/13/2018 |