

Mathematics-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Steepest Descent | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
![\includegraphics[width=0.55\linewidth]{Bild_Steilster_Abstieg_Aussage}](/inhalt/aussage/aussage1499/img8.png)
As shown in the figure, the search direction is orthogonal to
the level set through ![]() and touches the level set for a smaller
function value in
and touches the level set for a smaller
function value in ![]() .
.
The convergence of the sequence
![]() ,
generated by the the method of steepest descent,
can be shown under fairly general assumptions.
It is sufficient that
,
generated by the the method of steepest descent,
can be shown under fairly general assumptions.
It is sufficient that ![]() is bounded from below and
is bounded from below and
![]() is Lipschitz continuous in a
neighborhood
is Lipschitz continuous in a
neighborhood ![]() of the set
of the set
![]() , i.e.,
, i.e.,
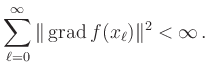
To ensure convergence of the algorithm, it is not necessary to
find the exact one-dimensional minimium in the direction of
![]() .
It is sufficient to use a non-optimal decent direction
.
It is sufficient to use a non-optimal decent direction ![]() and obtain merely
a reduction of the current function
and obtain merely
a reduction of the current function ![]() value which is proportional to
value which is proportional to
![]() .
.
| automatically generated 6/14/2016 |