
Mathematics-Online lexicon:
|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Complex Resistance in A.C. Networks | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
| resistor |
coil |
capacitor |
||||||
|
|
|
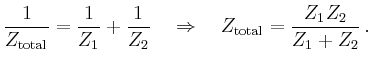
![]() is referred to as effective resistance,
is referred to as effective resistance,
![]() as reactance,
and
as reactance,
and ![]() as impedance.
as impedance.
![\includegraphics[width=.6\moimagesize]{komplexe_zahlen_schaltkreis.eps}](/inhalt/aussage/aussage1183/img19.png)
As an example, the (total) resistance of the circuit, shown in the figure, is
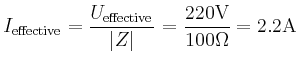
| automatically generated 5/ 5/2011 |