

Mathematics-Online lexicon:

|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Derivative | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
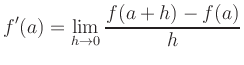
![\includegraphics[width=0.6\linewidth]{a_ableitung_bild_1}](/inhalt/aussage/aussage109/img4.png)
Geometrically, differentiability means that the slopes of the secants converge to the slope of the tangent given by
We also write
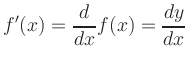
Higher derivatives are denoted by
![]() or
or
![]() , respectively.
, respectively.
We say that a function ![]() is differentiable on a set
is differentiable on a set ![]() if
if
![]() exists for all
exists for all ![]() .
.
| automatically generated 6/14/2016 |