
Mathematics-Online course: Preparatory Course Mathematics - Analysis - Differential Calculus
|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online course: Preparatory Course Mathematics - Analysis - Differential Calculus | ||
Derivative | ||
| [previous page] [next page] | [table of contents][page overview] |
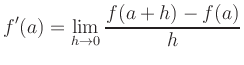
![\includegraphics[width=0.6\linewidth]{a_ableitung_bild_1}](/inhalt/aussage/aussage109/img4.png)
Geometrically, differentiability means that the slopes of the secants converge to the slope of the tangent given by
We also write
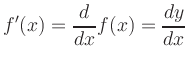
Higher derivatives are denoted by
![]() or
or
![]() , respectively.
, respectively.
We say that a function ![]() is differentiable on a set
is differentiable on a set ![]() if
if
![]() exists for all
exists for all ![]() .
.
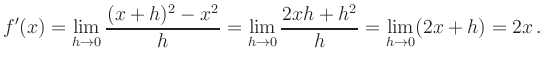
In general, with the aid of the binomial formula, we can compute the
derivative of an arbitrary monomial
![]() :
:
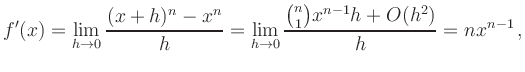
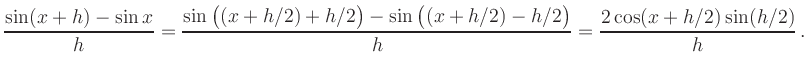
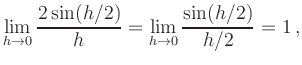
| [previous page] [next page] | [table of contents][page overview] |
| automatically generated 1/9/2017 |