Mathematics-Online course: Vector Calculus-Lines-Distance of Two Lines

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online course: Vector Calculus - Lines
	Distance of Two Lines

[previous page] [next page]

[table of contents][page overview]

The distance between two lines

and

which are not parallel and with parametric equations

$\displaystyle g : \vec{p} + t\vec{u} , t \in \mathbb{R}$

and

$\displaystyle h : \vec{q} + s\vec{v} , s \in \mathbb{R}$

is given by

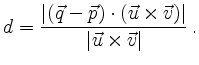
$\displaystyle d = \frac{\vert(\vec{q} - \vec{p}) \cdot (\vec{u} \times \vec{v})\vert} {\vert\vec{u} \times \vec{v}\vert}\, .$

This follows from the geometric properties of the dot and the cross product because the distance coincides with the distance of from the plane containing and the by translated line

Using the parallelepidial product the distance may be expressed as

$\displaystyle d = \frac{\vert[\overrightarrow{PQ},\vec{u},\vec{v}]\vert} {\vert\vec{u}\times\vec{v}\vert}\, ,$

where and are the points with location vector $\vec{p}$ and $\vec{q}$ rsp.

For parallel lines we have

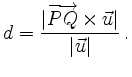
$\displaystyle d = \frac{\vert\overrightarrow{PQ}\times\vec{u}\vert} {\vert\vec{u}\vert}\, .$

$\includegraphics[width=11cm]{a_abstand_gerade_gerade_bild}$

Two lines are called skew lines if they are not parallel and if the distance between them is positive.

Denoting the position vectors of the points of minimal distance by

$\displaystyle \vec{x} = \vec{p} + s\vec{u},\quad \vec{y} = \vec{q} + t\vec{v}\,,$

then

$\displaystyle \overrightarrow{XY} = \overrightarrow{PQ} + t\vec{v} - s\vec{u}$

is orthogonal to both direction vectors, and, consequently, is parallel to

$\displaystyle \vec{c} = \vec{u}\times\vec{v}\, .$

Since the magnitude of a vector equals the absolute value of its scalar product with an parallel unit vector, it follows that

$\displaystyle d = \vert\overrightarrow{XY}\vert = \left\vert (\overrightarrow... ...overrightarrow{PQ} \cdot \frac{\vec{c}}{\vert\vec{c}\vert} \right\vert\, ,$

and we obtain the desired formula.

For parallel lines we can use the formula for the distance of a point from a line.

The distance between the lines

$\displaystyle g: \left(\begin{array}{c}1\\ 2\\ 3\end{array}\right)+ t\left(\be... ...3\\ 3\end{array}\right)+ t\left(\begin{array}{c}1\\ -2\\ 1\end{array}\right)$

amounts to

$\displaystyle d=\frac{\left\vert\left[\overrightarrow{PQ},\vec{u},\vec{v}\right]\right\vert} {\left\vert\vec{u}\times\vec{v}\right\vert}$	$\displaystyle =$	$\displaystyle \frac{ \left\vert\left(\left(\begin{array}{r}3\\ 3\\ 3\end{array}... ...ay}\right)\times \left(\begin{array}{r}1\\ -2\\ 1\end{array}\right)\right\vert}$
	$\displaystyle =$	$\displaystyle \frac{ \left\vert\left(\begin{array}{r}2\\ 1\\ 0\end{array}\right... ...t\vert} {\sqrt{(1-(-2))^2+(1-1)^2+((-2)-1)^2}} =\frac{6}{3\sqrt{2}}=\sqrt{2}\,.$

[previous page] [next page]

[table of contents][page overview]

automatically generated 10/30/2007