Mathematics-Online course: Linear Algebra-Analytic Geometry-Quadrics-Euclidean Normal Form of three-dimensional Quadrics

	[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff]
	Mathematics-Online course: Linear Algebra - Analytic Geometry - Quadrics
	Euclidean Normal Form of three-dimensional Quadrics

[previous page]

[table of contents][page overview]

There exist appropriate Cartesian coordinate systems with respect to which the equations defining quadrics have the following normal forms.

conical quadrics

normal form name

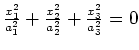$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+\frac{x_3^2}{a_3^2}=0$ point

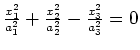$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}=0$ (double) cone

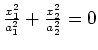$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}=0$ line

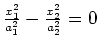$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}=0$ intersecting planes

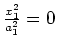$\frac{x_1^2}{a_1^2}=0$ coincident planes

central quadrics

normal form name

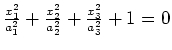$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+\frac{x_3^2}{a_3^2}+1=0$ (empty set)

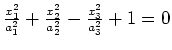$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}+1=0$ hyperboloid of 2 sheets

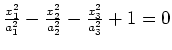$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}+1=0$ hyperboloid of 1 sheet

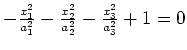$-\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}+1=0$ ellipsoid

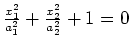$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+1=0$ (empty set)

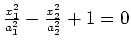$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}+1=0$ hyperbolic cylinder

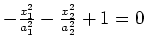$-\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}+1=0$ elliptic cylinder

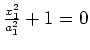$\frac{x_1^2}{a_1^2}+1=0$ (empty set)

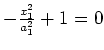$-\frac{x_1^2}{a_1^2}+1=0$ parallel planes

parabolic quadrics

normal form name

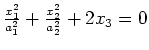$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+2x_3=0$ elliptic paraboloid

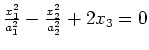$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}+2x_3=0$ hyperbolic paraboloid

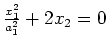$\frac{x_1^2}{a_1^2}+2x_2=0$ parabolic cylinder

The normal forms are uniquely determined up to permutation of subscripts and in the case of conical quadrics up to multiplication by a constant $c\ne 0$ .

The values are set to be positive and are called lengths of the principal axes of the quadric.

(double) cone intersecting planes

$\includegraphics[width=.4\moimagesize]{quadriken_kegel}$ $\includegraphics[width=.4\moimagesize]{quadriken_schneidende_ebenen}$

hyperboloid of 2 sheets hyperboloid of 1 sheet

$\includegraphics[width=.4\moimagesize]{quadriken_zweischaliges_hyperboloid}$ $\includegraphics[width=.4\moimagesize]{quadriken_einschaliges_hyperboloid}$

ellipsoid hyperbolic cylinder

$\includegraphics[width=.4\moimagesize]{quadriken_ellipsoid}$ $\includegraphics[width=.4\moimagesize]{quadriken_hyperbolischer_zylinder}$

elliptic cylinder elliptic paraboloid

$\includegraphics[width=.4\moimagesize]{quadriken_elliptischer_zylinder}$ $\includegraphics[width=.4\moimagesize]{quadriken_paraboloid}$

hyperbolic paraboloid parabolic cylinder

$\includegraphics[width=.4\moimagesize]{quadriken_hyperbolisches_paraboloid}$ $\includegraphics[width=.4\moimagesize]{quadriken_parabolischer_zylinder}$

(Authors: Burkhardt/Höllig/Hörner)

The quadric

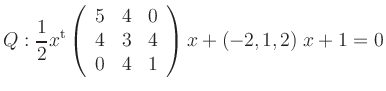
$\displaystyle Q: \frac{1}{2} x^{\operatorname t}\left(\begin{array}{rrr}5 & 4 & 0 \\ 4 & 3 & 4 \\ 0 & 4 & 1\end{array}\right)x+ \left(-2,1,2\right)x+1=0$

is to put into normal form.

The characteristical polynomial of the corresponding matrix,

$\displaystyle p(\lambda)=\lambda^3-9\lambda^2-9\lambda+81\,,$

has the zeros

$\displaystyle \lambda_1=9\,,\quad \lambda_2=3\,,\quad \lambda_3=-3\,.$

A basis of eigenvectors is

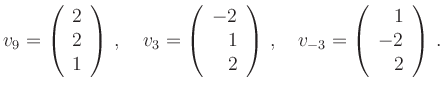
$\displaystyle v_9=\left(\begin{array}{r}2\\ 2\\ 1\end{array}\right)\,,\quad v_3... ...y}\right)\,,\quad v_{-3}=\left(\begin{array}{r}1\\ -2\\ 2\end{array}\right)\,.$

We obtain the following orthogonal transformation

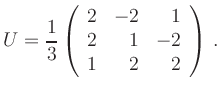
$\displaystyle U=\frac{1}{3}\left(\begin{array}{rrr} 2 & -2 & 1\\ 2 & 1 &-2\\ 1&2&2\end{array}\right)\,.$

Transforming the equation by

yields

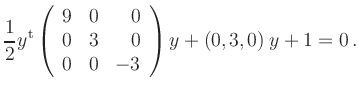
$\displaystyle \frac{1}{2} y^{\operatorname t}\left(\begin{array}{rrr}9 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & -3\end{array}\right)y+ \left(0,3,0\right)y+1=0\,.$

Completing squares gives

0	$\displaystyle =$	$\displaystyle 9y_1^2+3y_2^2-3y_3^2+6y_2+2$
	$\displaystyle =$	$\displaystyle 9y_1^2+3(y_2+1)^2-6y_2-3-3y_3^2+6y_2+2$
	$\displaystyle =$	$\displaystyle 9z_1^2+3z_2^2-3z_3^2-1$

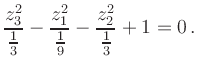
$\displaystyle \frac{z_3^2}{\frac{1}{3}}-\frac{z_1^2}{\frac{1}{9}}-\frac{z_2^2}{\frac{1}{3}}+1=0\,.$

Thus, the equation describes a hyperboloid of 1 sheet.

automatically generated 4/21/2005

normal form	name
$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+\frac{x_3^2}{a_3^2}=0$	point
$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}=0$	(double) cone
$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}=0$	line
$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}=0$	intersecting planes
$\frac{x_1^2}{a_1^2}=0$	coincident planes

(double) cone	intersecting planes

$\includegraphics[width=.4\moimagesize]{quadriken_kegel}$	$\includegraphics[width=.4\moimagesize]{quadriken_schneidende_ebenen}$

hyperboloid of 2 sheets	hyperboloid of 1 sheet

$\includegraphics[width=.4\moimagesize]{quadriken_zweischaliges_hyperboloid}$	$\includegraphics[width=.4\moimagesize]{quadriken_einschaliges_hyperboloid}$

ellipsoid	hyperbolic cylinder

$\includegraphics[width=.4\moimagesize]{quadriken_ellipsoid}$	$\includegraphics[width=.4\moimagesize]{quadriken_hyperbolischer_zylinder}$

elliptic cylinder	elliptic paraboloid

$\includegraphics[width=.4\moimagesize]{quadriken_elliptischer_zylinder}$	$\includegraphics[width=.4\moimagesize]{quadriken_paraboloid}$

hyperbolic paraboloid	parabolic cylinder

$\includegraphics[width=.4\moimagesize]{quadriken_hyperbolisches_paraboloid}$	$\includegraphics[width=.4\moimagesize]{quadriken_parabolischer_zylinder}$