
Mathematics-Online lexicon:
|
[home] [lexicon] [problems] [tests] [courses] [auxiliaries] [notes] [staff] |

|
|
Mathematics-Online lexicon: | ||
Gauss-Jordan algorithm | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | overview |
with a non-singular ![]() coefficient matrix
coefficient matrix ![]() . With equivalence
transformations it successively eliminates the unknowns
. With equivalence
transformations it successively eliminates the unknowns
until the coefficient matrix becomes the unit matrix and the right-hand side
contains the solution ![]() .
.
To implement the algorithm we combine the coefficient matrix and the
right-hand side to an
![]() matrix
matrix ![]() . Before the
. Before the
![]() -th elimination step this matrix has the form
-th elimination step this matrix has the form
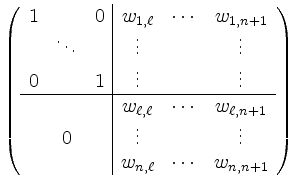
with modified entries ![]() .
.
The elimination of ![]() proceeds in three steps:
proceeds in three steps:
The third step generates zeros in positions
![]() , i.e.,
the dimension of the unit matrix in the upper left block increases by
one. Consequently, after
, i.e.,
the dimension of the unit matrix in the upper left block increases by
one. Consequently, after ![]() elimination steps, column
elimination steps, column ![]() of
of ![]() contains
the solution
contains
the solution ![]() .
.
| automatically generated 3/ 8/2007 |